• The Birth of the Principia
• Newton’s Preface
• Definitions
• Axioms, or Laws of Motion

Book I

Of the Motion of Bodies

• I Of the method of first and last ratios of quantities, by the help whereof we demonstrate the propositions that follow
• II Of the invention of centripetal forces
• III Of the motion of bodies in eccentric conic sections
• IV Of the finding of elliptic, parabolic, and hyperbolic orbits, from the focus given
• V How the orbits are to be found when neither focus is given
• VI How the motions are to be found in given orbits
• VII Concerning the rectilinear ascent and descent of bodies
• VIII Of the invention of orbits wherein bodies will revolve, being acted upon by any sort of centripetal force
• IX Of the motion of bodies in moveable orbits, and of the motion of the apsides
• X Of the motion of bodies in given superficies, and of the reciprocal motion of funependulous bodies
• XI Of the motion of bodies to each other with centripetal forces
• XII Of the attractive forces of spherical bodies
• XIII Of the attractive forces of bodies which are not of a spherical figure
• XIV Of the motion of very small bodies when agitated by centripetal forces tending to the several parts of any very great body

Book II

Of the Motion of Bodies (contd.)

• I Of the motion of bodies that are resisted in the ratio of velocity
• II Of the motion of bodies that are resisted in the duplicate ratio of their velocities
• III Of the motions of bodies which are resisted partly in the ratio of the velocities, and partly in the duplicate of the same ratio
• IV Of the circular motion of bodies in resisting mediums
• V Of the density and compression of fluids; and of hydrostatics
• VI Of the motion and resistance of funependulous bodies
• VII Of the motion of fluids and the resistance made to projected bodies
• VIII Of motion propagated through fluids
• IX Of the circular motion of fluids

Book III

The System of the World

Rules of Reasoning in Philosophy

Phenomena, or Appearances

Propositions I-XVI of the Motion of the Moon’s Nodes

General Scholium

Historical Background

The birth of the Principia may be traced back to a discussion in 1684 at the Royal Society. Astronomer Edmund Halley and architect Sir Christopher Wren suspected that there was an inverse square relation governing celestial motions based on Kepler's Third Law of elliptical orbits, but no one could prove it. They brought the question before Newton's arch rival Robert Hooke, who claimed that he could prove the inverse square law and all three of Kepler's laws. His claim was met with scepticism, and Wren offered a forty-shilling book as a prize for the correct proof within a two-month limit. Hooke failed to produce the calculation, and Halley travelled to Cambridge to ask for Newton's opinion. Newton responded with a typical lack of interest in work that he had already completed, that he had already solved the problem years before. He could not find the calculation among his papers and promised to send Halley a proof. Halley, suspecting the same bogus claim he had received from Hooke, left frustrated and returned to London. Three months later he received a nine page treatise from Newton, written in Latin, De Motu Corporum, or On the Motions of Bodies in Orbit. In it, Newton offers the correct proof of Kepler's laws in terms of an inverse square law of gravitation and his three laws of motion. Halley suggested publication, but Newton, reluctant to appear in print, refused. At Halley's insistence, Newton finally began writing and, with typical thoroughness, worked for 18 months revising and rewriting the short paper until it grew into three volumes. The Royal Society, having exhausted available funds on an extravagant edition of De Historia Piscium, or The History of Fishes, could not pay for the publication and so it was at Edmund Halley's expense that Philosophiæ Naturalis Principia Mathematica was finally published.

The Mathematical Principles of Natural Philosophy, or The Principia as it came to be commonly known, begins with the solid foundation on which the three books rest. Newton begins by defining the concepts of mass, motion (momentum), and three types of forces: inertial, impressed and centripetal. He also gives his definitions of absolute time, space, and motion, offering evidence for the existence of absolute space and motion in his famous "bucket experiment". These absolute concepts provoked great criticism from philosophers Leibnitz, Berkeley, and others, including Ernst Mach centuries later.  The three Laws of Motion are proposed, with consequences derived from them. The remainder of The Principia continues in rigorously logical Euclidean fashion in the form of propositions, lemmas, corollaries and scholia. Book One, Of The Motion of Bodies, applies the laws of motion  to the behaviour of bodies in various orbits. Book Two continues with the motion of resisted bodies in fluids,  and with the behaviour of fluids themselves. In the Third Book, The System of the World, Newton applies the Law of Universal Gravitation to the motion of planets, moons and comets within the Solar System. He explains a diversity of phenomena from this unifying concept, including the behaviour of Earth's tides, the precession of the equinoxes, and the irregularities in the moon's orbit.

The Principia brought Newton fame, publicity, and financial security. It established him, at the age of 45, as one of the greatest scientists in history.

Preface

NEWTON'S PREFACE to the FIRST EDITION.

Since the ancients (as we are told by Pappas), made great account of the science of mechanics in the investigation of natural things; and the moderns, lying aside substantial forms and occult qualities, have endeavoured to subject the phænomena of nature to the laws of mathematics, I have in this treatise cultivated mathematics so far as it regards philosophy. The ancients considered mechanics in a twofold respect; as rational, which proceeds accurately by demonstration; and practical. To practical mechanics all the manual arts belong, from which mechanics took its name. But as artificers do not work with perfect accuracy, it comes to pass that mechanics is so distinguished from geometry, that what is perfectly accurate is called geometrical; what is less so, is called mechanical. But the errors are not in the art, but in the artificers. He that works with less accuracy is an imperfect mechanic; and if any could work with perfect accuracy, he would be the most perfect mechanic of all; for the description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn; for it requires that the learner should first be taught to describe these accurately, before he enters upon geometry; then it shows how by these operations problems may be solved. To describe right lines and circles are problems, but not geometrical problems. The solution of these problems is required from mechanics; and by geometry the use of them, when so solved, is shown; and it is the glory of geometry that from those few principles, brought from without, it is able to produce so many things. Therefore geometry is founded in mechanical practice, and is nothing but that part of universal mechanics which accurately proposes and demonstrates the art of measuring. But since the manual arts are chiefly conversant in the moving of bodies, it comes to pass that geometry is commonly referred to their magnitudes, and mechanics to their motion. In this sense rational mechanics will be the science of motions resulting from any forces whatsoever, and of the forces required to produce any motions, accurately proposed and demonstrated. This part of mechanics was cultivated by the ancients in the five powers which relate to manual arts, who considered gravity (it not being a manual power, no otherwise than as it moved weights by those powers. Our design not respecting arts, but philosophy, and our subject not manual but natural powers, we consider chiefly those things which relate to gravity, levity, elastic force, the resistance of fluids, and the like forces, whether attractive or impulsive; and therefore we offer this work as the mathematical principles of philosophy; for all the difficulty of philosophy seems to consist in this – from the phænomena of motions to investigate the forces of nature, and then from these forces to demonstrate the other phænomena; and to this end the general propositions in the first and second book are directed. In the third book we give an example of this in the explication of the System of the World; for by the propositions mathematically demonstrated in the former books, we in the third derive from the celestial phænomena the forces of gravity with which bodies tend to the sun and the several planets. Then from these forces, by other propositions which are also mathematical, we deduce the motions of the planets, the comets, the moon, and the sea. I wish we could derive the rest of the phænomena of nature by the same kind of reasoning from mechanical principles; for I am induced by many reasons to suspect that they may all depend upon certain forces by which the particles of bodies, by some causes hitherto unknown, are either mutually impelled towards each other, and cohere in regular figures, or are repelled and recede from each other; which forces being unknown, philosophers have hitherto attempted the search of nature in vain; but I hope the principles here laid down will afford some light either to this or some truer method of philosophy.

In the publication of this work the most acute and universally learned Mr. Edmund Halley not only assisted me with his pains in correcting the press and taking care of the schemes, but it was to his solicitations that its becoming public is owing; for when he had obtained of me my demonstrations of the figure of the celestia1 orbits, he continually pressed me to communicate the same to the Roya1 Society, who afterwards, by their kind encouragement and entreaties, engaged me to think of publishing them. But after I had begun to consider the inequalities of the lunar motions, and had entered upon some other things relating to the laws and measures of gravity, and other forces; and the figures that would be described by bodies attracted according to given laws; and the motion of several bodies moving among themselves; the motion of bodies in resisting mediums; the forces, densities, and motions, of mediums; the orbits of the comets, and such like; deferred that publication till I had made a search into those matters, and could put forth the whole together. What relates to the lunar motions (being imperfect), I have put all together in the corollaries of Prop. 66, to avoid being obliged to propose and distinctly demonstrate the several things there contained in a method more prolix than the subject deserved, and interrupt the series of the several propositions. Some things, found out after the rest, I chose to insert in places less suitable, rather than change the number of the propositions and the citations. I heartily beg that what I have here done may be read with candour; and that the defects in a subject so difficult be not so much reprehended as kindly supplied, and investigated by new endeavours of my readers.

ISAAC NEWTON

Cambridge, Trinity College May 8, 1686.

NEWTONS PREFACE to the SECOND EDITION, 1713.

In the second edition the second section of the first book was enlarged. In the seventh section of the second book the theory of the resistances of fluids was more accurately investigated, and confirmed by new experiments. In the third book the moon's theory and the præcession of the equinoxes were more fully deduced from their principles; and the theory of the comets was confirmed by more examples of the calculation of their orbits, done also with greater accuracy.

NEWTONS PREFACE to the THIRD EDITION, 1726.

In this third edition the resistance of mediums is somewhat more largely handled than before; and new experiments of the resistance of heavy bodies falling in air are added. In the third book, the argument to prove that the moon is retained in its orbit by the force of gravity is enlarged on; and there are added new observations of Mr. Pound's of the proportion of the diameters of Jupiter to each other: there are, besides, added Mr. Kirk's observations of the comet in 1680; the orbit of that comet computed in an ellipsis by Dr. Halley; and the orbit of the comet in 1723 computed by Mr. Bradley.

Definitions

DEFINITION I.

The quantity of matter is the measure of the same, arising from its density and bulk conjunctly.

THUS air of double density, in a double space, is quadruple in quantity; in a triple space, sextuple in quantity. The same thing is to be understood of snow, and fine dust or powders, that are condensed by compression or liquefaction; and of all bodies that are by any caused whatever differently condensed. I have no regard in this place to a medium, if any such there is, that freely pervades the interstices between the parts of bodies. It is this quantity that I mean hereafter everywhere under the name of body or mass. And the same is known by the weight of each body; for it is proportional to the weight, as I have found by experiments on pendulums, very accurately made, which shall be shewn hereafter.

DEFINITION II.

The quantity of motion is the measure of the same, arising from the velocity and quantity of matter conjunctly.

The motion of the whole is the sum of the motions of all the parts; and therefore in a body double in quantity, with equal velocity, the motion is double; with twice the velocity, it is quadruple.

DEFINITION III.

The vis insita, or innate force of matter, is a power of resisting, by which every body, as much as in it lies, endeavours to persevere in its present state, whether it be of rest, or of moving uniformly forward in a right line.

This force is ever proportional to the body whose force it is; and differs nothing from the inactivity of the mass, but in our manner of conceiving it. A body, from the inactivity of matter, is not without difficulty put out of its state of rest or motion. Upon which account, this vis insita, may, by a most significant name, be called vis inertiæ, or force of inactivity. But a body exerts this force only, when another force, impressed upon it, endeavours to change its condition; and the exercise of this force may be considered both as resistance and impulse; it is resistance, in so far as the body, for maintaining its present state, withstands the force impressed; it is impulse, in so far as the body, by not easily giving way to the impressed force of another, endeavours to change the state of that other. Resistance is usually ascribed to bodies at rest, and impulse to those in motion; but motion and rest, as commonly conceived, are only relatively distinguished; nor are those bodies always truly at rest, which commonly are taken to be so.

DEFINITION IV.

An impressed force is an action exerted upon a body, in order to change its state, either of rest, or of moving uniformly forward in a right line.

This force consists in the action only; and remains no longer in the body when the action is over. For a body maintains every new state it acquires, by its vis inertiæ only. Impressed forces are of different origins as from percussion, from pressure, from centripetal force.

DEFINITION V.

A centripetal force is that by which bodies are drawn or impelled, or any way tend, towards a point as a centre.

Of this sort is gravity, by which bodies tend to the centre of the earth; magnetism, by which iron tends to the load-stone; and that force, whatever it is, by which the planets are perpetually drawn aside from the rectilinear motions, which otherwise they would pursue, and made to revolve in curvilinear orbits. A stone whirled about in a sling, endeavours to recede from the hand that turns it; and by that endeavour, distends the sling, and that with so much the greater force, as it is revolved with the greater velocity, and as soon as ever it is let go, flies away. That force which opposes itself to this endeavour, and by which the sling perpetually draws back the stone towards the hand, and retains it in its orbit, because it is directed to the hand as the centre of the orbit, I call the centripetal force. And the thing is to be understood of all bodies, revolved in any orbits. They all endeavour to recede from the centres of their orbits; and were it not for the opposition of a contrary force which restrains them to, and detains them in their orbits, which I therefore call centripetal, would fly off in right lines, with a uniform motion. A projectile, if it was not for the force of gravity, would not deviate towards the earth, but would go off from it in a right line, and that with an uniform motion, if the resistance of the air was taken away. It is by its gravity that it is drawn aside perpetually from its rectilinear course, and made to deviate towards the earth more or less, according to the force of its gravity, and the velocity of its motion. The less its gravity is, for the quantity of its matter, or the greater the velocity with which it is projected, the less will it deviate from a rectilinear course, and the farther it will go. If a leaden ball, projected from the top of a mountain by the force of gunpowder with a given velocity, and in a direction parallel to the horizon, is carried in a curve line to the distance of two miles before it falls to the ground; the same, if the resistance of the air were taken away, with a double or decuple velocity, would fly twice or ten times as far. And by increasing the velocity, we may at pleasure increase the distance to which it might be projected, and diminish the curvature of the line, which it might describe, till at last it should fall at the distance of 10, 30, or 90 degrees, or even might go quite round the whole earth before it falls; or lastly, so that it might never fall to the earth, but go forward into the celestial spaces, and proceed in its motion in infinitum. And after the same manner that a projectile, by the force of gravity, may be made to revolve in an orbit, and go round the whole earth, the moon also, either by the force of gravity, if it is endued with gravity, or by any other force, that impels it towards the earth, may be perpetually drawn aside towards the earth, out of the rectilinear way, which by its innate force it would pursue; and would be made to revolve in the orbit which it now describes; nor could the moon without some such force, be retained in its orbit. If this force was too small, it would not sufficiently turn the moon out of a rectilinear course: if it was too great, it would turn it too much, and draw down the moon from its orbit towards the earth. It is necessary, that the force be of a just quantity, and it belongs to the mathematicians to find the force, that may serve exactly to retain a body in a given orbit, with a given velocity; and vice versa, to determine the curvilinear way, into which a body projected from a given place, with a given velocity, may be made to deviate from its natural rectilinear way, by means of a given force.

The quantity of any centripetal force may be considered as of three kinds; absolute, accelerative, and motive.

 DEFINITION VI.

The absolute quantity of a centripetal force is the measure of the same proportional to the efficacy of the cause that propagates it from the centre, through the spaces round about.

Thus the magnetic force is greater in one load-stone and less in another according to their sizes and strength of intensity. 

DEFINITION VII.

The accelerative quantity of a centripetal force is the measure of the same, proportional to the velocity which it generates in a given time.

Thus the force of the same load-stone is greater at a less distance, and less at a greater: also the force of gravity is greater in valleys, less on tops of exceeding high mountains; and yet less (as shall hereafter be shown), at greater distances from the body of the earth; but at equal distances, it is the same everywhere; because (taking away, or allowing for the resistance of the air), it equally accelerates all falling bodies, whether heavy or light, great or small.

 DEFINITION VIII.

The motive quantity of a centripetal force, is the measure of the same, proportional to the motion which it generates in a given time.

Thus the weight is greater in a greater body, less in a less body; and, in the same body, it is greater near to the earth, and less at remoter distances. This sort of quantity is the centripetency, or propension of the whole body towards the centre, or, as I may say, its weight; and it is always known by the quantity of an equal and contrary force just sufficient to hinder, the descent of the body.

These quantities of forces, we may, for brevity's sake, call by the names of motive, accelerative, and absolute forces; and, for distinction's sake, consider them, with respect to the bodies that tend to the centre; to the places of those bodies; and to the centre of force towards which they tend; that is to say, I refer the motive force to the body as an endeavour and propensity of the whole towards a centre, arising from the propensities of the several parts taken together; the accelerative force to the place of the body, as a certain power or energy diffused from the centre to all places around to move the bodies that are in them; and the absolute force to the centre, as endued with some cause, without which those motive forces would not be propagated through the spaces round about; whether that cause be some central body (such as is the load-stone, in the centre of the magnetic force, or the earth in the centre of the gravitating force), or anything else that does not yet appear. For I here design only to give a mathematical notion of those forces, without considering their physical causes and seats.

Wherefore the accelerative force will stand in the same relation to the motive, as celerity does to motion. For the quantity of motion arises from the celerity drawn into the quantity of matter; and the motive force arises from the accelerative force drawn into the same quantity of matter. For the sum of the actions of the accelerative force, upon the several particles of the body, is the motive force of the whole. Hence it is, that near the surface of the earth, where the accelerative gravity, or force productive of gravity, in all bodies is the same, the motive gravity or the weight is as the body: but if we should ascend to higher regions, where the accelerative gravity is less, the weight would be equally diminished, and would always be as the product of the body, by the accelerative gravity. So in those regions, where the accelerative gravity is diminished into one half, the weight of a body two or three times less, will be four or six times less.

I likewise call attractions and impulses, in the same sense, accelerative, and motive; and use the words attraction, impulse or propensity of any sort towards a centre, promiscuously, and indifferently, one for another; considering those forces not physically, but mathematically: wherefore, the reader is not to imagine, that by those words, I anywhere take upon me to define the kind, or the manner of any action, the causes or the physical reason thereof, or that I attribute forces, in a true and physical sense, to certain centres (which are only mathematical points); when at any time I happen to speak of centres as attracting, or as endued with attractive powers.

SCHOLIUM.

Hitherto I have laid down the definitions of such words as are less known, and explained the sense in which I would have them to be understood in the following discourse. I do not define time, space, place and motion, as being well known to all. Only I must observe, that the vulgar conceive those quantities under no other notions but from the relation they bear to sensible objects. And thence arise certain prejudices, for the removing of which, it will be convenient to distinguish them into absolute and relative, true and apparent, mathematical and common.

I. Absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external, and by another name is called duration: relative, apparent, and common time, is some sensible and external (whether accurate or unequable) measure of duration by the means of motion, which is commonly used instead of true time; such as an hour, a day, a month, a year.

II. Absolute space, in its own nature, without regard to anything external, remains always similar and immovable. Relative space is some movable dimension or measure of the absolute spaces; which our senses determine by its position to bodies; and which is vulgarly taken for immovable space; such is the dimension of a subterraneaneous, an æreal, or celestial space, determined by its position in respect of the earth. Absolute and relative space, are the same in figure and magnitude; but they do not remain always numerically the same. For if the earth, for instance, moves, a space of our air, which relatively and in respect of the earth remains always the same, will at one time be one part of the absolute space into which the air passes; at another time it will be another part of the same, and so, absolutely understood, it will be perpetually mutable.

III. Place is a part of space which a body takes up, and is according to the space, either absolute or relative. I say, a part of space; not the situation nor the external surface of the body. For the places of equal solids are always equal; but their superfices, by reason of their dissimilar figures, are often unequal. Positions properly have no quantity, nor are they so much the places themselves, as the properties of places. The motion of the whole is the same thing with the sum of the motions of the parts; that is, the translation of the whole, out of its place, is the same thing with the sum of the translations of the parts out of their places; and therefore the place of the whole is the same thing with the sum of the places of the parts, and for that reason, it is internal, and in the whole body.

IV. Absolute motion is the translation of a body from one absolute place into another; and relative motion, the translation from one relative place into another. Thus in a ship under sail, the relative place of a body is that part of the ship which the body possesses; or that part of its cavity which the body fills, and which therefore moves together with the ship: and relative rest is the continuance of the body in the same part of the ship, or of its cavity. But real, absolute rest, is the continuance of the body in the same part of that immovable space, in which the ship itself, its cavity, and all that it contains, is moved. Wherefore if the earth is really at rest, the body, which relatively rests in the ship, will really and absolutely move with the same velocity which the ship has on the earth. But if the earth also moves, the true and absolute motion of the body will arise, partly from the true motion of the earth, in immovable space; partly from the relative motion of the ship on the earth; and if the body moves also relatively in the ship; its true motion will arise, partly from the true motion of the earth, in immovable space, and partly from the relative motions as well of the ship on the earth, as of the body in the ship; and from these relative motions will arise the relative motion of the body on the earth. As if that part of the earth, where the ship is, was truly moved toward the east, with a velocity of 10010 parts; while the ship itself, with fresh gale, and full sails, is carried towards the west, with a velocity expressed by 10 of those parts; but a sailor walks in the ship towards the east, with 1 part of the said velocity; then the sailor will be moved truly in immovable space towards the east, with a velocity of 10001 parts, and relatively on the earth towards the west, with a velocity of 9 of those parts.

Absolute time, in astronomy, is distinguished from relative, by the equation or correlation of the vulgar time. For the natural days are truly unequal, though they are commonly considered as equal and used for a measure of time; astronomers correct this inequality for their more accurate deducing of the celestial motions. It may be, that there is no such thing as an equable motion, whereby time may be accurately measured. All motions may be accelerated and retarded, but the true, or equable, progress of absolute time is liable to no change. The duration or perseverance of the existence of things remains the same, whether the motions are swift or slow, or none at all: and therefore, it ought to be distinguished from what are only sensible measures thereof; and out of which we collect it, by means of the astronomical equation. The necessity of which equation, for determining the times of a phænomenon, is evinced as well from the experiments of the pendulum clock, as by eclipses of the satellites of Jupiter.

As the order of the parts of time is immutable, so also is the order of the parts of space. Suppose those parts to be moved out of their places, and they will be moved (if the expression may be allowed) out of themselves. For times and spaces are, as it were, the places as well of themselves as of all other things. All things are placed in time as to order of succession; and in space as to order of situation. It is from their essence or nature that they are places; and that the primary places of things should be moveable, is absurd. These are therefore the absolute places; and translations out of those places, are the only absolute motions.

But because the parts of space cannot be seen, or distinguished from one another by our senses, therefore in their stead we use sensible measures of them. For from the positions and distances of things from any body considered as immovable, we define all places; and then with respect to such places, we estimate all motions, considering bodies as transferred from some of those places into others. And so, instead of absolute places and motions, we use relative ones; and that without any inconvenience in common affairs; but in philosophical disquisitions, we ought to abstract from our senses, and consider things themselves, distinct from what are only sensible measures of them. For it may be that there is no body really at rest, to which the places and motions of others may be referred.

But we my distinguish rest and motion, absolute and relative, one from the other by their properties, causes and effects. It is a property of rest, that bodies really at rest do rest in respect to one another. And therefore as it is possible, that in the remote regions of the fixed stars, or perhaps far beyond them, there may be some body absolutely at rest; but impossible to know, from the position of bodies to one another in our regions whether any of these do keep the same position to that remote body; it follows that absolute rest cannot be determined from the position of bodies in our regions.

It is a property of motion, that the parts, which retain given positions to their wholes, do partake of the motions of those wholes. For all the parts of revolving bodies endeavour to recede from the axis of motion; and the impetus of bodies moving forward, arises from the joint impetus of all the parts. Therefore, if surrounding bodies are moved, those that are relatively at rest within them, will partake of their motion. Upon which account, the true and absolute motion of a body cannot be determined by the translation of it from those which only seem to rest; for the external bodies ought not only to appear at rest, but to be really at rest. For otherwise, all included bodies, beside their translation from near the surrounding ones, partake likewise of their true motions; and though that translation were not made they would not be really at rest, but only seem to be so. For the surrounding bodies stand in the like relation to the surrounded as the exterior part of a whole does to the interior, or as the shell does to the kernel; but, if the shell moves, the kernel will also move, as being part of the whole, without any removal from near the shell.

A property, near akin to the preceding, is this, that if a place is moved, whatever is placed therein moves along with it; and therefore a body, which is moved from a place in motion, partakes also of the motion of its place. Upon which account, all motions, from places in motion, are no other than parts of entire and absolute motions; and every entire motion is composed of the motion of the body out of its first place, and the motion of this place out of its place; and so on, until we come to some immovable place, as in the before-mentioned example of the sailor. Wherefore, entire and absolute motions can be no otherwise determined than by immovable places; and for that reason I did before refer those absolute motions to immovable places, but relative ones to movable places. Now no other places are immovable but those that, from infinity to infinity, do all retain the same given position to one another; and upon this account must ever remain unmoved; and do thereby constitute immovable space.

The causes by which true, and relative motions are distinguished, one from the other, are the forces impressed upon bodies to generate motion. True motion is neither generated nor altered, but by some force impressed upon the body moved; but relative motion may be generated or altered without any force impressed upon the body. For it is sufficient only to impress some force on other bodies with which the former is compared, that by their giving way, that relation may be changed, in which the relative rest or motion of this other body did consist. Again, true motion suffers always some change from any force impressed upon, the moving body; but relative motion does not necessarily undergo any change by such forces. For if the same forces are likewise impressed on those other bodies, with which the comparison is made, that the relative position may be preserved, then that condition will be preserved in which the relative motion consists. And therefore any relative motion may be changed when the true motion remains unaltered, and the relative may be preserved when the true suffers some change. Upon which accounts, true motion does by no means consist in such relations.

The effects which distinguish absolute from relative motion are, the forces of receding from the axis of circular motion. For there are no such forces in a circular motion purely relative, but in a true and absolute circular motion, they are greater or less, according to the quantity of the motion. If a vessel, hung by a long cord, is so often turned about that the cord is strongly twisted, then filled with water, and held at rest together with the water; after, by the sudden action of another force, it is whirled about the contrary way, and while the cord is untwisting itself, the vessel continues, for some time in this motion; the surface of the water will at first be plain, as before the vessel began to move: but the vessel, by gradually communicating its motion to the water, will make it begin sensibly to evolve, and recede by little and little from the middle, and ascend to the sides of the vessel, forming itself into a concave figure (as I have experienced), and the swifter the motion becomes, the higher will the water rise, till at last, performing its revolutions in the same times with the vessel, it becomes relatively at rest in it. This ascent of the water shows its endeavour to recede from the axis of its motion; and the true and absolute circular motion of the water, which is here directly contrary to the relative, discovers itself, and may be measured by this endeavour. At first, when the relative motion of the water in the vessel was greatest, it produced no endeavour to recede from the axis; the water showed no tendency to the circumference, nor any ascent towards the sides of the vessel, but remained of a plain surface, and therefore its true circular motion had not yet begun. But afterwards, when the relative motion of the water had decreased, the ascent thereof towards the sides of the vessel proved its endeavour to recede from the axis; and this endeavour showed the real circular motion of the water perpetually increasing, till it had acquired its greatest quantity, when the water rested relatively in the vessel. And therefore this endeavour, does not depend upon any translation of the water in respect of the ambient bodies, nor can true circular motion be defined by such translation. There is only one real circular motion of any one revolving body, corresponding to only one power of endeavouring to recede from its axis of motion, as its proper and adequate effect; but relative motions, in one and the same body, are innumerable, according to the various relations it bears to external bodies, and like other relations, are altogether destitute of any real effect, any otherwise than they may partake of that one only true motion. And therefore in their system who suppose that our heavens, revolving below the sphere of the fixed stars, carry the planets along with them; the several parts of those heavens and the planets, which are indeed relatively at rest in their heavens, do yet really move. For they change their position one to another (which never happens to bodies truly at rest), and being carried together with their heavens, partake of their motions, and as parts of revolving wholes, endeavour to recede from the axis of their motions.

Wherefore relative quantities are not the quantities themselves, whose names they bear, but those sensible measures of them (either accurate or inaccurate), which are commonly used instead of the measured quantities themselves. And if the meaning of words is to be determined by their use, then by the names time, space, place and motion, their measures are properly to be understood; and the expression will be unusual, and purely mathematical, if the measured quantities themselves are meant. Upon which account, they do strain the sacred writings, who there interpret those words for the measured quantities. Nor do those less defile the purity of mathematical and philosophical truths, who confound real quantities themselves with their relations and vulgar measures.

It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motion of particular bodies from the apparent; because the parts of that immovable space, in which those motions are performed, do by no means come under the observation of our senses. Yet the thing is not altogether desperate; for we have some arguments to guide us, partly from the apparent motions, which are the differences of the true motions; partly from the forces, which are the causes and effects of the true motion. For instance, if two globes, kept at a given distance one from the other by means of a cord that connects them, were revolved about their common centre of gravity, we might, from the tension of the cord, discover the endeavour of the globes to recede from the axis of their motion, and from thence we might compute the quantity of their circular motions. And then if any equal forces should be impressed at once on the alternate faces of the globes to augment or diminish their circular motions, from the increase or decrease of the tension of the cord, we might infer the increment or decrement of their motions; and thence would be found on what faces those forces ought to be impressed, that the motions of the globes might be most augmented; that is, we might discover their hindermost faces, or those which, in the circular motion, do follow. But the faces which follow being known and consequently the opposite ones that precede, we should likewise know the determination of their motions. And thus we might find both the quantity and the determination of this circular motion, even in an immense vacuum, where there was nothing external or sensible with which the globes could be compared. But now, if in that space some remote bodies were placed the kept always a given position one to another, as the fixed stars do in our regions, we could not indeed determine from the relative translation of the globes among those bodies, whether the motion did belong to the globes or to the bodies. But if we observed the cord, and found that its tension was that very tension which the motions f the globes required, we might conclude the motion to be in the globes, and the bodies to be at rest; and then, lastly, from the translation of the globes among the bodies, we should find the determination of their motions. But how we are to collect the true motions from their causes, effects, and apparent differences; and, vice versa, how from the motions, either true or apparent, we may come to the knowledge of their causes and effects, shall be explained more at large in the following tract. For to this end it was that I composed it.

AXIOMS, OR LAWS OF MOTION

LAW I.

Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.

PROJECTILES persevere in their motions, so far as they are not retarded by the resistance of the air, or impelled downwards by the force of gravity. A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time.

LAW II.

The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.

If any force generates a motion, a double force will generate double the motion, a triple force triple the motion, whether that force be impressed altogether and at once, or gradually and successively. And this motion (being always directed the same way with the generating force), if the body moved before, is added to or subtracted from the former motion, according as they directly conspire with or are directly contrary to each other; or obliquely joined, when they are oblique, so as to produce a new motion compounded from the determination of both.

LAW III.

To every action there is always opposed an equal reaction; or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

Whatever draws or presses another is as much drawn or pressed by that other. If you press a stone with your finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse (if I may so say) will be equally drawn back towards the stone: for the distended rope, by the same endeavour to relax or unbend itself, will draw the horse as much towards the stone as it does the stone towards the horse, and will obstruct the progress of the one as much as it advances that of the other.

If a body impinges upon another, and by its force change the motion of the other, that body also (became of the quality of, the mutual pressure) will undergo an equal change, in its own motion, towards the contrary part. The changes made by these actions are equal, not in the velocities but in the motions of bodies; that is to say, if the bodies are not hindered by any other impediments. For, because the motions are equally changed, the changes of the velocities made towards contrary parts are reciprocally proportional to the bodies. This law takes place also in attractions, as will be proved in the next scholium.

COROLLARY I.

A body by two forces conjoined will describe the diagonal of a parallelogram, in the same time that it would describe the sides, by those forces apart.

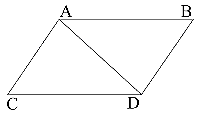
If a body in a given time, by the force M impressed apart in the place A, should with an uniform motion be carried from A to B; and by the force N impressed apart in the same place, should be carried from A to C; complete the parallelogram ABCD, and, by both forces acting together, it will in the same time be carried in the diagonal from A to D. For since the force N acts in the direction of the line AC, parallel to BD, this force (by the second law) will not at all alter the velocity generated by the other force M, by which the body is carried towards the line BD. The body therefore will arrive at the line BD in the same time, whether the force N be impressed or not; and therefore at the end of that time it will be found somewhere in the line BD. By the same argument, at the end of the same time it will be found somewhere in the line CD. Therefore it will be found in the point D, where both lines meet. But it will move in a right line from A to D, by Law I.

COROLLARY II.

And hence is explained the composition of any one direct force AD, out of any two oblique forces AC and CD; and, on the contrary, the resolution of any one direct force AD into two oblique forces AC and CD: which composition and resolution are abundantly confirmed from mechanics.

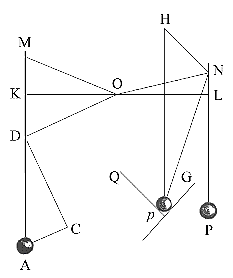
As if the unequal radii OM and ON drawn from the centre O of any wheel, should sustain the weights A and P by the cords MA and NP; and the forces of those weights to move the wheel were required. Through the centre O draw the right line KOL, meeting the cords perpendicularly in K and L; and from the centre O, with OL the greater of the distances OK and OL, describe a circle, meeting the cord MA in D: and drawing OD, make AC parallel and DC perpendicular thereto. Now, it being indifferent whether the points K, L, D, of the cords be fixed to the plane of the wheel or not, the weights will have the same effect whether they are suspended from the points K and L, or from D and L. Let the whole force of the weight A be represented by the line AD, and let it be resolved into the forces AC and CD; of which the force AC, drawing the radius OD directly from the centre, will have no effect to move the wheel: but the other force DC, drawing the radius DO perpendicularly, will have the same effect as if it drew perpendicularly the radius OL equal to OD; that is, it will have the same effect as the weight P, if that weight is to the weight A as the force DC is to the force DA; that is (because of the similar triangles ADC, DOK), as OK to OD or OL. Therefore the weights A and P, which are reciprocally as the radii OK and OL that lie in the same right line, will be equipollent, and so remain in equilibrio; which is the well known property of the balance, the lever, and the wheel. If either weight is greater than in this ratio, its force to move the wheel will be so much greater.

If the weight p, equal to the weight P, is partly suspended by the cord Np, partly sustained by the oblique plane pG; draw pH, NH, the former perpendicular to the horizon, the latter to the plane pG; and if the force of the weight p tending downwards is represented by the line pH, it may be resolved into the forces pN, HN. If there was any plane pQ, perpendicular to the cord pN, cutting the other plane pG in a line parallel to the horizon, and the weight p was supported only by those planes pQ, pG, it would press those planes perpendicularly with the forces pN, HN; to wit, the plane pQ with the force pN, and the plane pG with the force HN. And therefore if the plane pQ was taken away, so that the weight might stretch the cord, because the cord, now sustaining the weight, supplies the place of the plane that was removed, it will be strained by the same force pN which pressed upon the plane before. Therefore, the tension of this oblique cord pN will be to that of the other perpendicular cord PN as pN to pH. And therefore if the weight p is to the weight A in a ratio compounded of the reciprocal ratio of the least distances of the cords PN, AM, from the centre of the wheel, and of the direct ratio of pH to pN, the weights will have the effect towards moving the wheel and will therefore sustain each other; as any one may find by experiment.

But the weight p pressing upon those two oblique planes, may be considered as a wedge between the two internal surfaces of a body split by it; and hence the forces of the wedge and the mallet may be determined; for because the force with which the weight p presses the plane pQ is to the force with which the same, whether by its own gravity, or by the blow of a mallet, is impelled in the direction of the line pH towards both the planes, as pN to pH; and to the force with which it presses the other plane pG, as pN to NH. And thus the force of the screw may be deduced from a like resolution of forces; it being no other than a wedge impelled with the force of a lever. Therefore the use of this Corollary spreads far and wide, and by that diffusive extent the truth thereof is farther confirmed. For on what has been said depends the whole doctrine of mechanics variously demonstrated by different authors. For from hence are easily deduced the forces of machines, which are compounded of wheels, pullies, levers, cords, and weights, ascending directly or obliquely, and other mechanical powers; as also the force of the tendons to move the bones of animals.

COROLLARY III.

The quantity of motion, which is collected by taking the sum of the motions directed towards the same parts, and the difference of those that are directed to contrary parts, suffers no change from the action of bodies among themselves.

For action and its opposite re-action are equal, by Law III, and therefore, by Law II, they produce in the motions equal changes towards opposite parts. Therefore if the motions are directed towards the same parts, whatever is added to the motion of the preceding body will be subducted from the motion of that which follows; so that the sum will be the same as before. If the bodies meet, with contrary motions, there will be an equal deduction from the motions of both; and therefore the difference of the motions directed towards opposite parts will remain the same.

Thus if a spherical body A with two parts of velocity, is triple of a spherical body B which follows in the same right line with ten parts of velocity, the motion of A will be to that of B as 6 to 10. Suppose, then, their motions to be of 6 parts and of 10 parts, and the sum will be 16 parts. Therefore, upon the meeting of the bodies, if A acquire 3, 4, or 5 parts of motion, B will lose as many; and therefore after reflexion A will proceed with 9, 10, or 11 parts, and B with 7, 6, or 5 parts; the sum remaining always of 16 parts as before. If the body A acquire 9, 10, 11, or 12 parts of motion, and therefore after meeting proceed with 15, 16, 17, or 18 parts, the body B, losing so many parts as A has got, will either proceed with 1 part, having lost 9, or stop and remain at rest, as having lost its whole progressive motion of 10 parts: or it will go back with 1 part, having not only lost its whole motion, but (if I may so say) one part more; or it will go back with 2 parts, because a progressive motion of 12 parts is taken off. And so the sums of the conspiring motions 15+1, or 16+0, and the differences of the contrary motions 17-1 and 18-2, will always be equal to 16 parts, as they were before the meeting and reflexion of the bodies. But the motions being known with which the bodies proceed after reflexion, the velocity of either will be also known, by taking the velocity after to the velocity before reflexion, as the motion after is to the motion before. As in the last case, where the motion of the body A was of 6 parts before reflexion and of 18 parts after, and the velocity was of 2 parts before reflexion, the velocity thereof after reflexion will be found to be of 6 parts; by saying, as the 6 parts of motion, before to 18 parts after, so are 2 parts of velocity before reflexion to 6 parts after.

But if the bodies are either not spherical, or, moving in different right lines, impinge obliquely one upon the other, and their motions after reflexion are required, in those cases we are first to determine the position of the plane that touches the concurring bodies in the point of concourse; the. The motion of each body (by Corol. II) is to be resolved into two, one perpendicular to that plane, and the other parallel to it. This done, because the bodies act upon each other in the direction of a line perpendicular to this plane, the parallel motions are to be retained the same after reflexion as before; and to the perpendicular motions we are to assign equal changes towards the contrary parts; in such manner that the sum of the conspiring and the difference of the contrary motions may remain the same as before. From such kind of reflexions also sometimes arise the circular motions of bodies about their own centres. But these are cases which I do not consider in what follows; and it would be too tedious to demonstrate every particular that relates to this subject.

COROLLARY IV.

The common centre of gravity of two or more bodies does not alter its state of motion or rest by the actions of the bodies among themselves; and therefore the common centre of gravity of all bodies acting upon each other (excluding outward actions and impediments) is either at rest, or moves uniformly in a right line.

For if two points proceed with an uniform motion in right lines, and their distance be divided in a given ratio, the dividing point will be either at rest, or proceed uniformly in a right line. This is demonstrated hereafter in Lem. XXIII and its Corol., when the points are moved in the same plane; and by a like way of arguing, it may be demonstrated when the points are not moved in the same plane. Therefore if any number of bodies move uniformly in right lines, the common centre of gravity of any two of them is either at rest, or proceeds uniformly in a right line; because the line which connects the centres of those two bodies so moving is divided at that common centre in a given ratio. In like manner the common centre of those two and that of a third body will be either at rest or moving uniformly in a right line because at that centre the distance between the common centre of the two bodies, and the centre of this last, is divided in a given ratio. In like manner the common centre of these three, and of a forth body, is either at rest, or moves uniformly in a right line; because the distance between the common centre of the three bodies, and the centre of the fourth is there also divided in a given ratio, and so on in infinitum. Therefore, in a system of bodies where there is neither any mutual action among themselves, nor any foreign force impressed upon them from without, and which consequently move uniformly in right lines, the common centre of gravity of them all is either at rest or moves uniformly forward in a right line.

Moreover, in a system of two bodies mutually acting upon each other, the distances between their centres and the common centre of gravity of both are reciprocally as the bodies, the relative motions of those bodies, whether of approaching to or of receding from that centre, will be equal among themselves. Therefore since the changes which happen to motions are equal and directed to contrary parts, the common centre of those bodies, by their mutual action between themselves, is neither promoted nor retarded, nor suffers any change as to its state of motion or rest. But in a system of several bodies, because the common centre of gravity of any two acting mutually upon each other suffers no change in its state by that action; and much less the common centre of gravity of the others with which that action does not intervene; but the distance between those two centres is divided by the common centre of gravity of all the bodies into parts reciprocally proportional to the total sums of those bodies whose centres they are; and therefore while those two centres retain their state of motion or rest, the common centre of all does also retain its state: it is manifest that the common centre of all never suffers any change in the state of its motion or rest from the actions of any two bodies between themselves. But in such a system all the actions of the bodies among themselves either happen between two bodies, or are composed of actions interchanged between some two bodies; and therefore they do never produce any alteration in the common centre of all as to its state of motion or rest. Wherefore since that centre, when the bodies do not act mutually one upon another, either is at rest or moves uniformly forward in some right line, it will, notwithstanding the mutual actions of the bodies among themselves, always persevere in its state, either of rest, or of proceeding uniformly in a right line, unless it is forced out of this state by the action of some power impressed from without upon the whole system. And therefore the same law takes place in a system consisting of many bodies as in one single body, with regard to their persevering in their state of motion or of rest. For the progressive motion, whether of one single body, or of a whole system of bodies, is always to be estimated from the motion of the centre of gravity.

COROLLARY V.

The motions of bodies included in a given space are the same among themselves, whether that space is at rest, or moves uniformly forwards in a right line without any circular motion.

For the differences of the motions tending towards the same parts, and the sums of those that tend towards contrary parts, are, at first (by supposition), in both cases the same; and it is from those sums and differences that the collisions and impulses do arise with which the bodies mutually impinge one upon another. Wherefore (by Law II), the effects of those collisions will be equal in both cases; and therefore the mutual motions of the bodies among themselves in the one case will remain equal to the mutual motions of the bodies among themselves in the other. A clear proof of which we have from the experiment of a ship; where all motions happen after the same manner, whether the ship is at rest, or is carried uniformly forwards in a right line.

COROLLARY VI.

If bodies, any how moved among themselves, are urged in the direction of parallel lines by equal accelerative forces, they will all continue to move among themselves, after the same manner as if they had been urged by no such forces.

For these forces acting equally (with respect to the quantities of the bodies to be moved), and in the direction of parallel lines, will (by Law II) move all the bodies equally (as to velocity), and therefore will never produce any change in the positions or motions of the bodies among themselves.

SCHOLIUM.

Hitherto I have laid down such principles as have been received by mathematicians, and are confirmed by abundance of experiment. By the first two Laws and the first two Corollaries, Galileo discovered that the descent of bodies observed the duplicate ratio of the time, and that the motion of projectiles was in the curve of a parabola; experience agreeing with both, unless so far as these motions are a little retarded by the resistance of the air. When a body is falling, the uniform force of its gravity acting equally, impresses, in equal particles of time, equal forces upon that body, and therefore generates equal velocities; and in the whole time impresses a whole force, and generates a whole velocity proportional to the time. And the spaces described in proportional times are as the velocities and the times conjunctly; that is, in a duplicate ratio of the times. And when a body is thrown upwards, its uniform gravity impresses forces and takes off velocities proportional to the times; and the times of ascending to the greatest heights are as the velocities to be taken off, and those heights are as the velocities and the times conjunctly, or in the duplicate ratio of the velocities. And if a body be projected in any direction, the motion arising from its projection as compounded with the motion arising from its gravity.

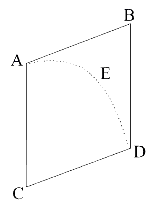
As if the body A by its motion of projection alone could describe in a given time the right line AB, and with its motion of falling alone could describe in the same time the altitude AC; complete the parallelogram ABDC, and the body by that compounded motion will at the end of the time be found in the place D; and the curve line AED, which that body describes, will be a parabola, to which the right line AB will be a tangent in A; and whose ordinate BD will be as the square of the line AB. On the same Laws and Corollaries depend those things which have been demonstrated concerning the times of the vibration of pendulums, and are confirmed by the daily experiments of pendulum clocks. By the same, together with the third Law, Sir Christ. Wren, Dr. Wallis, and Mr. Huygens, the greatest geometers of our times, did severally determine the rules of the congress and reflexion of hard bodies, and much about the same time communicated their discoveries to the Royal Society, exactly agreeing among themselves as to those rules. Dr. Wallis, indeed, was something more early in the publication; then followed Sir Christopher Wren, and, lastly, Mr. Huygens. But Sir Christopher Wren confirmed the truth of the thing before the Royal Society by the experiment of pendulums, which Mr. Mariotte soon after thought fit to explain in a treatise entirely upon that subject. But to bring this experiment to an accurate agreement with the theory, we are to have a due regard as well to the resistance of the air as to the elastic force of the concurring bodies.

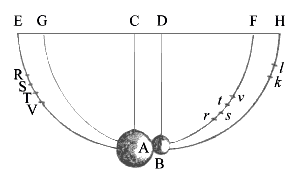
Let the spherical bodies A, B be suspended by the parallel and equal strings AC, BD, from the centres C, D. About these centres, with those intervals, describe the semicircles EAF, GBH, bisected by the radii CA, DB. Bring the body A to any point R of the arc EAF, and (withdrawing the body B) let it go from thence, and after one oscillation suppose it to return to the point V: then RV will be the retardation arising from the resistance of the air. Of this RV let ST be a fourth part, situated in the middle, to wit, so as RS and TV may be equal, and RS may be to ST as 3 to 2 then will ST represent very nearly the retardation during the descent from S to A. Restore the body B to its place: and, supposing the body A to be let fall from the point S, the velocity thereof in the place of reflexion A, without sensible error will be the same as if it had descended in vacuo from the point T. Upon which account this velocity may be represented by the chord of the arc TA. For it is a proposition well known to geometers, that the velocity of a pendulous body in the lowest point is as the chord of the arc which it has described in its descent. After reflexion, suppose the body A comes to the place s, and the body B to the place k. Withdraw the body B, and find the place v, from which if the body A, being let go, should after one oscillation return to the place r, st may be fourth part of rv, so placed in the middle thereof as to leave rs equal to tv, and let the chord of the arc tA represent the velocity which the body A had in the place A immediately after reflexion. For t will be the true and correct place to which the body A should have ascended, if the resistance of the air had been taken off. In the same way we are to correct the place k to which the body B ascends, by finding the place l to which it should have ascended in vacuo. And thus everything may be subjected to experiment, in the same manner as if we were really placed in vacuo. These things being done, we are to take the product (if I may so say) of the body A, by the chord of the arc TA (which represents its velocity), that we may have its motion in the place A immediately before reflexion; and then by the chord of the arc tA, that we may have its motion in the place A immediately after reflexion. And so we are to take the product of the body B by the chord of the arc Bl, that we may have the motion of the same immediately after reflexion. And in like manner, when two bodies are let go together from different places, we are to find the motion of each, as well before as after reflexion; and then we may compare the motions between themselves, and collect the effects of the reflexion. Thus trying the thing with pendulums of ten feet, in unequal as well as equal bodies, and making the bodies to concur after a descent through large spaces, as of 8, 12, or 16 feet, I found always, without an error of 3 inches, that when the bodies concurred together directly, equal changes towards the contrary parts were produced in their motions, and, of consequence, that the action and reaction were always equal. As if the body A impinged upon the body B at rest with 9 parts of motion, and losing 7, proceeded after reflexion with 2, the body B was carried backwards with those 7 parts. If the bodies concurred with contrary motions, A with twelve parts of motion, and B with six, then if A receded with 2, B receded with 8; to wit, with a deduction of 14 parts of motion on each side. For from the motion of A subducting twelve parts, nothing will remain; but subducting 2 parts more, a motion will be generated of 2 parts towards the contrary way; and so, from the motion of the body B of 6 parts, subducting 14 parts, a motion is generated of 8 parts towards the contrary way. But if the bodies were made both to move towards the same way, A, the swifter, with 14 parts of motion, B, the slower, with 5, and after reflexion A went on with 5, B likewise went on with 14 parts; 9 parts being transferred from A to B. And so in other cases. By the congress and collision of bodies, the quantity of motion, collected from the sum of the motions directed towards the same way, or from the difference of those that were directed towards contrary ways, was ever changed. For the error of an inch or two in measures may be easily ascribed to the difficulty of executing everything with accuracy. It was not easy to let go the two pendulums so exactly together that the bodies should impinge one upon the other in the lowermost place AB; nor to mark the places s and k, to which the bodies ascended after congress. Nay, and some errors, too, might have happened from the unequal density of the parts of the pendulous bodies themselves, and from the irregularity of the texture proceeding from other causes.

But to prevent an objection that may perhaps be alledged against the rule, for the proof of which this experiment was made, as if this rule did suppose that the bodies were either absolutely hard, or at least perfectly elastic (whereas no such bodies are to be found in nature), I must add, that the experiments we have been describing, by no means depending upon that quality of hardness, do succeed as well in soft as in hard bodies. For if the rule is to be tried in bodies not perfectly hard, we are only to diminish the reflexion such a certain proportion as the quantity of the elastic force requires. By the theory of Wren and Huygens, bodies absolutely hard return one from another with the same velocity with which they meet. But this may be affirmed with more certainty of bodies perfectly elastic. In bodies imperfectly elastic the velocity of the return is to be diminished together with the elastic force; because that force (except when the parts of bodies are bruised by their congress, or suffer some such extension as happens under the strokes of a hammer) is (as far as I can perceive) certain and determined, and makes the bodies to return one from the other with a relative velocity, which is in a given ratio to that relative velocity with which they met. This I tried in balls of wool, made up tightly, and strongly compressed. For, first, by letting go the pendulous bodies, and measuring their reflexion, I determined the quantity of their elastic force; and then, according to this force, estimated the reflexions that ought to happen in other cases of congress. And with this computation other experiments made afterwards did accordingly agree; the balls always receding one from the other with a relative velocity, which was to the relative velocity with which they met as about 5 to 9. Balls of steel returned with almost the same velocity: those of cork with a velocity something less; but in balls of glass the proportion was as about 15 to 16. And thus the third Law, so far as it regards percussions and reflexions, is proved by a theory exactly agreeing with experience.

In attractions, I briefly demonstrate the thing after this manner. Suppose an obstacle is interposed to hinder the progress of any two bodies A, B, mutually attracting one the other: then if either body, as A, is more attracted towards the other body B, than that other body B is towards the first body A, the obstacle will be more strongly urged by the pressure of the body A than by the pressure of the body B, and therefore will not remain in equilibrio: but the stronger pressure will prevail, and will make the system of the two bodies, together with the obstacle, to move directly towards the parts of which B lies; and in free spaces, to go forward in infinitum with a motion perpetually accelerated; which is absurd and contrary to the first Law. For, by the first Law, the system ought to persevere in its state of rest, or of moving uniformly forward in a right line; and therefore the bodies must equally press the obstacle, and be equally attracted one by the other. I made the experiment on the loadstone and iron. If these, placed apart in proper vessels, are made to float by one another in standing water, neither of them will propel the other; but, by being equally attracted, they will sustain each other's pressure, and rest at last in an equilibrium.

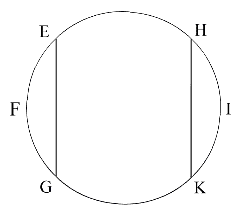
So the gravitation betwixt the earth and its parts is mutual. Let the earth FI be cut by any plane EG into two parts EGF and EGI, and their weights one towards the other will be mutually equal. For if by another plane HK, parallel to the former EG, the greater part EGI is cut into two parts EGKH and HKI, whereof HKI is equal to the part EFG, first cut off, it is evident that the middle part EGKH, will have no propension by its proper weight towards either side, but will hang as it were, and rest in an equilibrium betwixt both. But the one extreme part HKI will with its whole weight bear upon and press the middle part towards the other extreme part EGF; and therefore the force with which EGI, the sum of the parts HKI and EGKH, tends towards the third part EGF, is equal to the weight of the part HKI, that is, to the weight of the third part EGF. And therefore the weights of the two parts EGI and EGF, one towards the other, are equal, as I was to prove. And indeed if those weights were not equal, the whole earth floating in the nonresisting æther would give way to the greater weight, and, retiring from it, would be carried off in infinitum.

And as those bodies are equipollent in the congress and reflexion, whose velocities are reciprocally as their innate force, so in the use of mechanic instruments those agents are equipollent, and mutually sustain each the contrary pressure of the other, whose velocities, estimated according to the determination of the forces, are reciprocally as the forces.

So those weights are of equal force to move the arms of a balance; which during the play of the balance are reciprocally as their velocities upwards and downwards; that is, if the ascent or descent is direct, those weights are of equal force, which are reciprocally as the distances of the points at which they are suspended from the axis of the balance; but if they are turned aside by the interposition of oblique planes, or other obstacles, and made to ascend or descend obliquely, those bodies will be equipollent, which are reciprocally as the heights of their ascent and descent taken according to the perpendicular; and that on account of the determination of gravity downwards.

And in like manner in the pully, or in a combination of pullies, the force of a hand drawing the rope directly, which is to the weight, whether ascending directly or obliquely, as the velocity of the perpendicular ascent of the weight to the velocity of the hand that draws the rope, will sustain the weight.

In clocks and such like instruments, made up from a combination of wheels, the contrary forces that promote and impede the motion of the wheels, if they are reciprocally as the velocities of the parts of the wheel on which they are impressed, will mutually sustain the one the other.

The force of the screw to press a body is to the force of the hand that turns the handles by which it is moved as the circular velocity of the handle in that part where it is impelled by the hand is to the progressive velocity of the screw towards the pressed body.

The form by which the wedge presses or drives the two parts of the wood it cleaves are to the force of the mallet upon the wedge as the progress of the wedge in the direction of the force impressed upon it by the mallet is to the velocity with which the parts of the wood yield to the wedge, in the direction of lines perpendicular to the sides of the wedge. And the like account is to be given of all machines.

The power and use of mechanics consist only in this, that by diminishing the velocity we may augment the force, and the contrary: from whence in all sorts of proper machines, we have the solution of this problem; To move a given weight with a given power, or with a given force to overcome any other given resistance. For if machines are so contrived that the velocities of the agent and resistant are reciprocally as their forces, the agent will just sustain the resistant, but with a greater disparity of velocity will overcome it. So that if the disparity of velocities is so great as to overcome all that resistance which commonly arises either from the attrition of contiguous bodies as they slide by one another, or from the cohesion of continuous bodies that are to be separated, or from the weights of bodies to be raised, the excess of the force remaining, after all those resistances are overcome, will produce acceleration of motion proportional thereto, as well in the parts of the machine as in the resisting body. But to treat of mechanics is not my present business. I was only willing to show by those examples the great extent and certainty of the third Law of motion. For if we estimate the action of the agent from its force and velocity conjunctly, and likewise the reaction of the impediment conjunctly from the velocities of its several parts, and from the forces of resistance arising from the attrition, cohesion, weight, and acceleration of those parts, the action and reaction in the use of all sorts of machines will be found always equal to one another. And so far as the action is propagated by the intervening instruments, and at last impressed upon the resisting body, the ultimate determination of